站点设定
产品
功率
变压器
汽车
资源
![YouTube preview image]()
![YouTube preview image]()
![YouTube preview image]()
![YouTube preview image]()
视频库

Cx Family Common Mode Chokes

0402CT Low Profile Chip Inductors

XAL7050 High-inductance Shielded Power Inductors

XGL4020 Ultra-low DCR Power Inductors
Student Support
Learn more about magnetics, request free samples or ask our engineers a question.
Get Support
Quality
安全认证

 (1)
(1)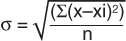 (2)
(2)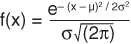 (3)
(3)
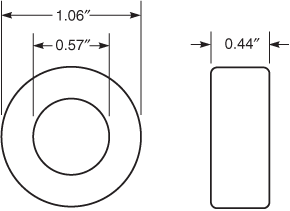
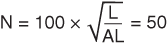 (4)
(4)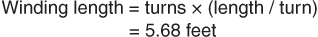 (5)
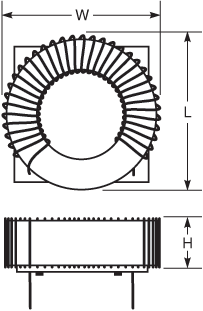
(5)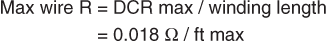 (6)
(6)
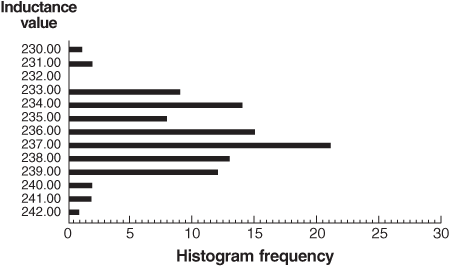
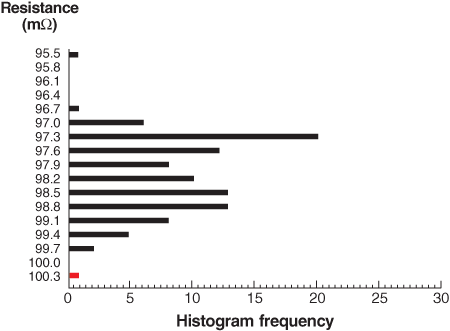
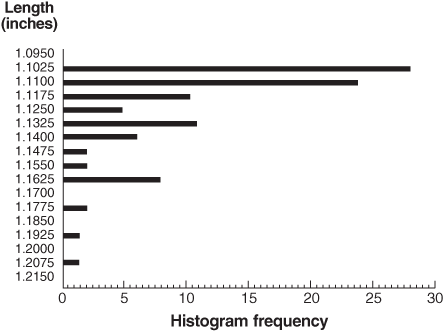
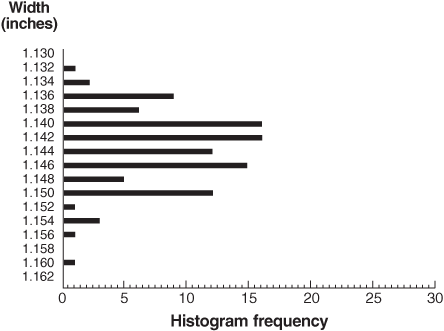
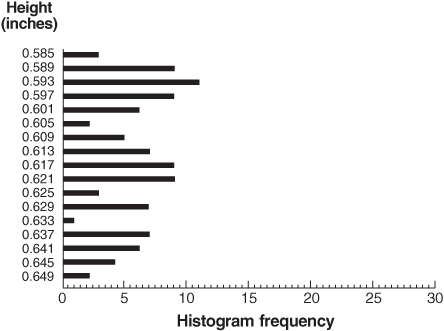
 (7)
(7)