사이트 설정
제품
전력
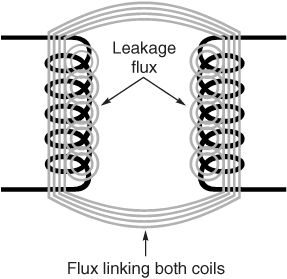
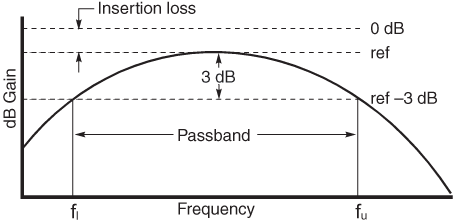
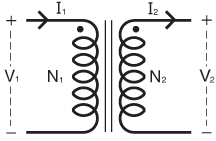
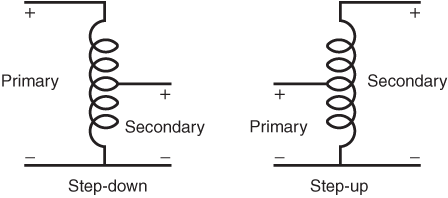
트랜스포머
자동차용
리소스
![YouTube preview image]()
![YouTube preview image]()
![YouTube preview image]()
![YouTube preview image]()
모델 및 레이아웃 도구
비디오 라이브러리

Cx Family Common Mode Chokes

0402CT Low Profile Chip Inductors

XAL7050 High-inductance Shielded Power Inductors

XGL4020 Ultra-low DCR Power Inductors
Student Support
Learn more about magnetics, request free samples or ask our engineers a question.
Get Support
품질
안전 인증