サイトの設定
製品
電力
トランス
車載
リソース
![YouTube preview image]()
![YouTube preview image]()
![YouTube preview image]()
![YouTube preview image]()
モデル&レイアウトツール
ビデオライブラリ

Cx Family Common Mode Chokes

0402CT Low Profile Chip Inductors

XAL7050 High-inductance Shielded Power Inductors

XGL4020 Ultra-low DCR Power Inductors
Student Support
Learn more about magnetics, request free samples or ask our engineers a question.
Get Support
Quality
安全認証
会社情報

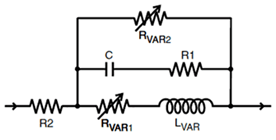
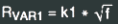 use LAPLACE=+1/{L1_K1}/(-S*S/4/PI^2)^0.25
For
use LAPLACE=+1/{L1_K1}/(-S*S/4/PI^2)^0.25
For 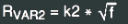 use LAPLACE=+1/{L1_K2}/(-S*S/4/PI^2)^0.25
For
use LAPLACE=+1/{L1_K2}/(-S*S/4/PI^2)^0.25
For 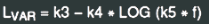 use LAPLACE=+1/(S*1e-6*({L1_K3} - ({L1_K4}*LOG({L1_K5}*(abs(S)/(2*pi))))))
use LAPLACE=+1/(S*1e-6*({L1_K3} - ({L1_K4}*LOG({L1_K5}*(abs(S)/(2*pi)))))).png)